Brownian Crystallisation (Diffusion-Limited Aggregation)

Overview

This project investigates Brownian crystallisation using a diffusion-limited aggregation (DLA) model. Particles undergo random walks on a two-dimensional lattice and irreversibly bind upon contact with a growing solid cluster, forming emergent crystalline and fractal structures.

The simulation explores how simple stochastic rules at the microscopic level lead to complex macroscopic structure — a central theme in statistical physics and non-equilibrium systems.

Physical Model

• Particles perform discrete two-dimensional Brownian motion
• Motion occurs on a finite square lattice
• Particles stick irreversibly upon first contact with the aggregate
• The aggregate acts as a growing absorbing boundary

This model captures the essential physics of crystallisation and pattern formation in diffusion-dominated regimes, relevant to crystal growth, electrochemical deposition, and colloidal aggregation.

Implementation

• Monte Carlo simulation of multi-particle random walks
• Vectorized NumPy operations for efficient state updates
• Explicit tracking of particle trajectories and aggregate geometry
• Frame-by-frame visualization and animation generation

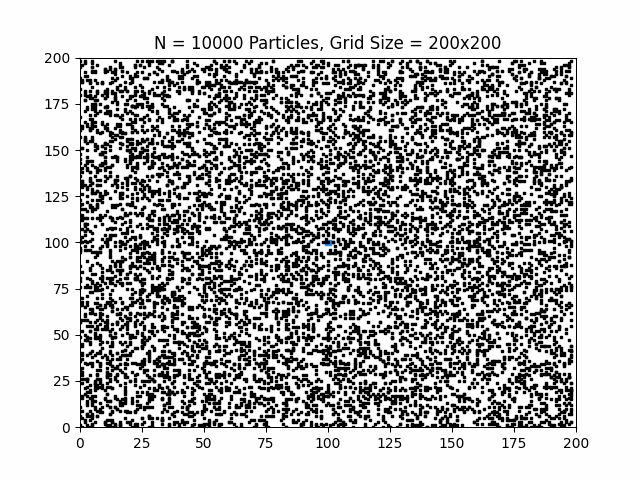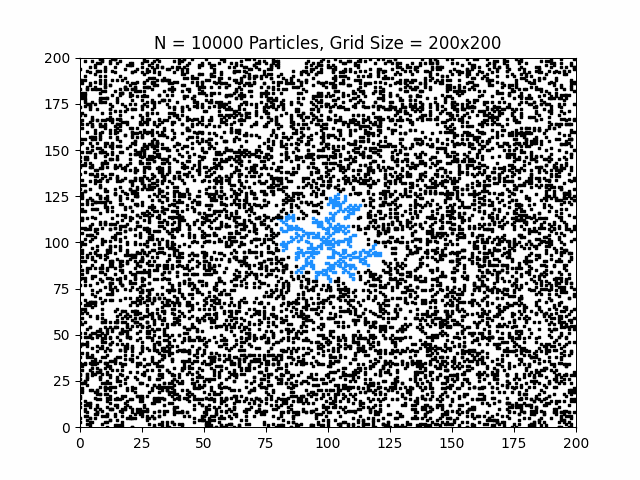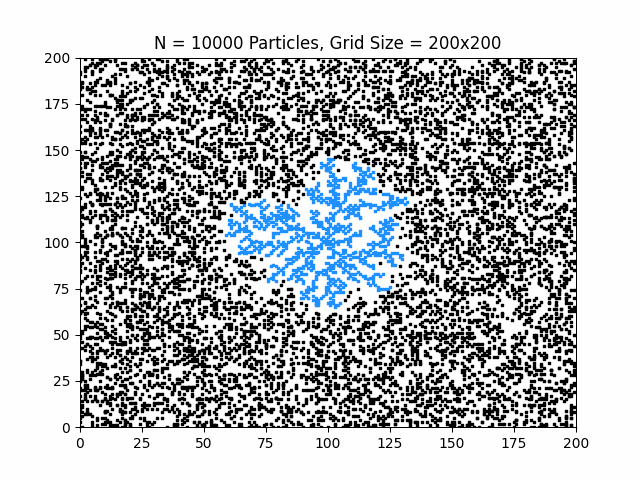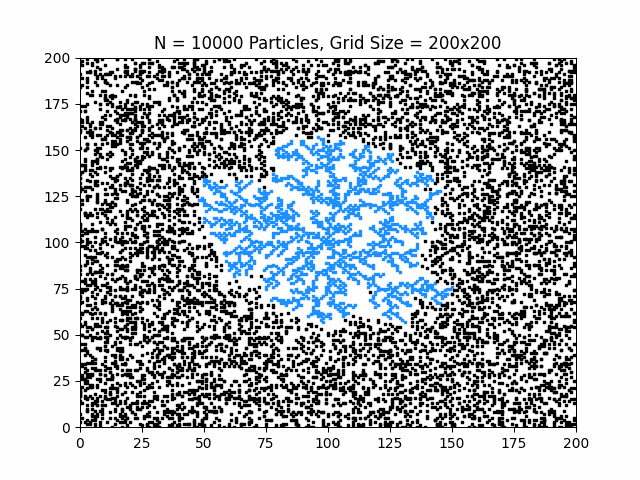
The animation above shows particles diffusing through the lattice and progressively attaching to the growing crystal, revealing the characteristic branching morphology of diffusion-limited growth.

Key Observations

• Growth is highly anisotropic despite isotropic diffusion
• Branching structures emerge naturally from stochastic motion
• Aggregate morphology depends sensitively on particle density and lattice size
• The resulting crystal exhibits fractal-like geometry

Why This Matters

Diffusion-limited aggregation provides a minimal yet powerful framework for understanding non-equilibrium structure formation. Variants of this model appear in:

• Crystal growth and solidification
• Electrodeposition and corrosion
• Colloidal physics and soft matter
• Pattern formation in biological systems

This project emphasizes how physically meaningful behavior can emerge from simple probabilistic rules — a recurring theme across physics, materials science, and complex systems.

Tools & Techniques

• Python
• NumPy
• Matplotlib
• Monte Carlo methods
• Stochastic simulation